Nền tảng của deep learning - Multi-layer Perceptron

Mục lục:

1. Mở đầu
2. Một số kí hiệu cần biết
3. Từ input tới output
4. Kết bài

1. Mở đầu

Ở phần 1 của series Deep learning cơ bản, chúng ta đã tìm hiểu về perceptron - mô hình đơn giản nhất của một artificial neuron (tế bào thần kinh nhân tạo). Trong phần tiếp theo này, nhóm sẽ giới thiệu tới các bạn một ví dụ của mạng neural network đơn giản được tạo ra từ các liên kết giữa các perceptron và là nền tảng để hiểu các mạng khác phức tạp hơn trong DL. Mạng neural network này có tên là Multi-layer Perceptron (MLP) và một ví dụ của nó như hình dưới.

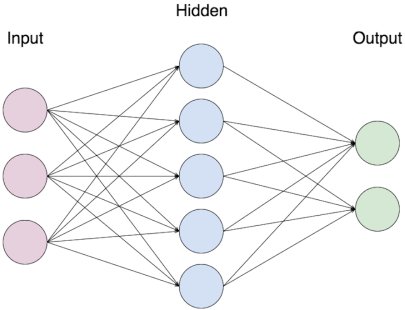
Hình 1. Multi-layer Perceptron

Gọi là Multi-layer Perceptron (perceptron nhiều lớp) bởi vì nó là tập hợp của các perceptron chia làm nhiều nhóm, mỗi nhóm tương ứng với một layer. Trong hình trên ta có một ANN với 3 lớp: Input layer (lớp đầu vào), Output layer (lớp đầu ra) và Hidden layer (lớp ẩn). Thông thường khi giải quyết một bài toán ta chỉ quan tâm đến input và output của một model, do vậy trong MLP nói riêng và ANN nói chung ngoài lớp Input và Output ra thì các lớp neuron ở giữa được gọi chung là Hidden (ẩn không phải là không nhìn thấy mà đơn giản là không quan tâm đến).

2. Một số kí hiệu cần biết

Để dễ hình dung, người ta thường gọi lớp Input là lớp thứ nhất (kí hiệu $l=1$) cứ thế tăng dần cho tới lớp output (trong Hình 1 là $l=3$). Ta sẽ nói MLP này có số lớp là $L=3$. Mỗi hình tròn là biểu trưng cho một neuron (trong trường hợp này là perceptron) do đó đối với lớp thứ 2 ta nói nó có $n=5$ neuron, lớp thứ 3 có $n=2$ neuron. Đối với lớp input thì mỗi hình tròn chỉ là đại diện cho một giá trị input chứ không ta không tính toán gì ở đây và được gọi là input neuron. Để biểu diễn một MLP bằng công thức toán, người ta thường sử dụng các kí hiệu như sau (Các kí hiệu này cũng được sử dụng cho các mạng ANN khác) :

• Các giá trị input thường được kí hiệu là $x_1, x_2, x_3, …, x_{n_x}$ với MLP có $n_x$ input.
• Đối với từng neuron, giá trị output của neuron thứ $k$ của lớp thứ $l$ được kí hiệu là $a_{k}^{l}$. Ví dụ output của neuron thứ 1 (tính từ trên xuống) của lớp thứ 2 sẽ là $a_{1}^{(2)}$, phía trên sẽ là số thứ tự lớp phía dưới là thứ tự neuron. Ngoài lớp Input ra thì ta có thể dễ dàng thấy là output của lớp này sẽ là input cho lớp kế tiếp.
• Như đã giới thiệu ở bài trước, mỗi mũi tên nối giữa các neuron của 2 lớp liền kề nhau đại diện cho một liên kết gửi-nhận thông tin với độ mạnh yếu được quyết định bởi một giá trị $w$ (weight). Ta gọi giá trị $w$ của liên kết giữa neuron thứ $k$ ở lớp thứ $l-1$ với neuron thứ $j$ ở lớp kế tiếp $l$ là $w_{jk}^{(l)}$. Chỗ này rất dễ nhầm lẫn nên các bạn chú ý, ví dụ liên kết giữa neuron thứ 1 ở lớp thứ 2 với neuron thứ 2 ở lớp thứ 3 sẽ viết là $w_{21}^{(3)}$, ở phía trên là thứ tự lớp của neuron nhận tín hiệu vào, phía dưới là thứ tự của mỗi neuron trong từng lớp. Số thứ tự của neuron nhận tín hiệu viết trước và neuron gửi tín hiệu viết sau.
• Cuối cùng, các giá trị ouput được kí hiệu là $\hat{y_1}, \hat{y_2}, …,\hat{y_{n_y}}$ với $n_y$ là số output.

3. Từ input tới output

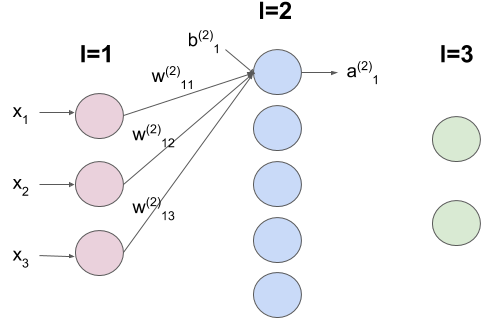
Hình 2. Kí hiệu liên quan đến neuron thứ 1 của lớp thứ 2

Sử dụng các kí hiệu như trên chúng ta sẽ biểu diễn quá trình tính toán từ input cho ra output của MLP 3 lớp trong Hình 1. Với lớp $l=1$ thì chỉ là lớp của các giá trị input nên ta không tính toán gì ở đây. Với lớp $l=2$ ta sẽ tính output của từng neuron. Bắt đầu với neuron thứ 1 của lớp $l=2$ như trong Hình 2, như đã tìm hiểu ở phần 1 đầu tiên chúng ta sẽ tính tổng ($z$, cách kí hiệu giống như với $a$) của các input tới đã được điều chỉnh độ mạnh yếu nhờ các giá trị $w$ :

$$z_{1}^{(2)} = 1w_0 + w_{11}^{(2)}x_1 + w_{12}^{(2)}x_2 + w_{13}^{(2)}x_3 = \sum_{k=1}^{3} w_{1k}^{(l)}x_k + w_0$$

Về giá trị $w_0$ (gọi là bias, do đó còn được kí hiệu là $b_{1}^{(2)}$ như Hình 2) các bạn có thể xem lại ở phần 1. Thường thì giá trị của bias là đặc trưng cho từng neuron. Ta đã biết nếu $z$ vượt qua một ngưỡng nhất định thì neuron sẽ phát ra một output còn không thì sẽ không output gì cả. Để quyết định một neuron có output hay không thì trong Deep Learning người ta sử dụng một số hàm số được gọi chung là Activation function. Nhóm sẽ giới thiệu kĩ hơn về các Activation function trong một dịp khác. Ở phần 1 ta đã sử dụng một hàm gọi là step function, còn ở đây giả sử ta sử dụng một hàm số thông dụng khác là hàm Sigmoid như sau:

$$\sigma(z) = \frac{1}{1+e^{-z}} = \frac{e^z}{e^z+1}$$

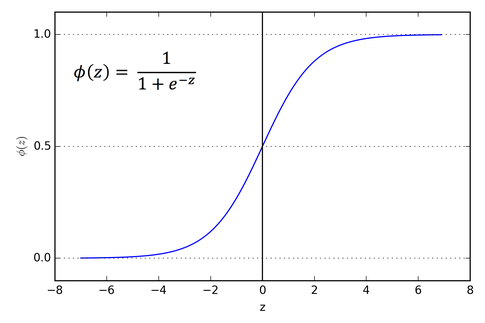
Hình 2. Đồ thị của hàm số sigmoid

Như ta thấy nếu $z$ nhỏ hơn một ngưỡng nhất định thì giá trị output của hàm sigmoid $\sigma$ (đọc là sigma) sẽ gần với 0 và nếu $z$ đủ lớn thì giá trị ouput sẽ gần với 1. Sử dụng hàm sigmoid này ta sẽ tính được giá trị output của neuron thứ 1 của lớp $l=2$ như sau:

$$a_{1}^{(2)} = \sigma(z_{1}^{(2)}) = \sigma(\sum_{k=1}^{3} w_{1k}^{(2)}x_k + w_0)$$

Và ta có thể làm tương tự như vậy đối với các neuron tiếp theo trong lớp Hidden $l=2$ và lớp Output $l=3$. Ta có thể thấy các tính toán trên giống hệt nhau cho các neuron trong cùng một lớp. Vì lý do đó mà ta có thể tính toán song song (parallel processing) nhiều neuron trong một lớp để tăng tốc độ. Điều đó dẫn tới việc trong DL GPU hay được sử dụng để tăng tốc độ tính toán (training + testing). Một CPU thông thường có khoảng vài đến vài chục core với xung nhịp (frequency) mỗi core lớn còn một GPU thông thường có khoảng vài trăm tới vài nghìn core với xung nhịp mỗi core nhỏ hơn. Với những tính toán đơn giản như trên thì không cần xung nhịp quá lớn do vậy GPU với số core gấp nhiều lần CPU sẽ giúp training nhanh hơn nhiều nhờ vào tính toán song song.
Để dễ hình dung về tính toán song song ta có thể biểu diễn các tính toán trên theo một dạng khác. Nếu bạn nào đã học đại số tuyến tính thì thay vì viết $z_i$ là tổng của các $w_ix_i$ thì ta có thể biểu diễn thành tích vô hướng của hai vector như sau (bạn nào chưa biết thì có thể xem qua link này):

$$z_{1}^{(2)} = \left[ {\begin{array}{cccc} w_{11}^{(2)} & w_{12}^{(2)} & w_{13}^{(2)} \\ \end{array} } \right] \left[ {\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} } \right] + b_{1}^{(2)} = w_{1}^{(2)T}x + b_{1}^{(2)}$$

Trong đó, $w_{1}^{(2)} = \left[ {\begin{array}{c} w_{11}^{(2)} \\ w_{12}^{(2)} \\ w_{13}^{(2)} \end{array} } \right]$ và $x = \left[ {\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array} } \right]$ lần lượt là cách viết theo dạng vector gồm tất cả các weight của neuron thứ 1 thuộc lớp $l=2$ và tất cả input $x$. Áp dụng tương tự với các neuron khác trong lớp, ta có thể viết gộp lại cách tính các giá trị output của tất cả các neuron trong lớp $l=2$ như sau:

$$Z^{(2)} = \left[ {\begin{array}{ccc} w_{11}^{(2)} & w_{12}^{(2)} & w_{13}^{(2)} \\ w_{21}^{(2)} & w_{22}^{(2)} & w_{23}^{(2)} \\ w_{31}^{(2)} & w_{32}^{(2)} & w_{33}^{(2)} \\ w_{41}^{(2)} & w_{42}^{(2)} & w_{43}^{(2)} \\ w_{51}^{(2)} & w_{52}^{(2)} & w_{53}^{(2)} \end{array} } \right] \left[ {\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} } \right] + \left[ {\begin{array}{c} b_{1}^{(2)} \\ b_{2}^{(2)} \\ b_{3}^{(2)} \\ b_{4}^{(2)} \\ b_{5}^{(2)} \end{array} } \right] = \left[ {\begin{array}{c} -w_{1}^{(2)T}- \\ -w_{2}^{(2)T}- \\ -w_{3}^{(2)T}- \\ -w_{4}^{(2)T}- \\ -w_{5}^{(2)T}- \end{array} } \right] \left[ {\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} } \right] + \left[ {\begin{array}{c} b_{1}^{(2)} \\ b_{2}^{(2)} \\ b_{3}^{(2)} \\ b_{4}^{(2)} \\ b_{5}^{(2)} \end{array} } \right] = W^{(2)T}X + b^{(2)}$$

Ở đây, $W^{(2)}$ ($W$ được viết hoa) được gọi là weight matrix (ma trận weight) và $b^{(2)}$ là bias vector của lớp $l=2$. Trong ví dụ ta đang xét thì $W^{(2)}$ là ma trận có $3\times 5$ chiều (dimension), vector $x$ có 3 chiều, vector $b$ có 5 chiều (mỗi neuron có 1 bias) và vector $z$ có 5 chiều. Các bạn có thể nhớ đơn giản số chiều của ma trận $W^{(2)}$ là $3\times 5$ vì nó output ra một vector có chiều là 5 (lớp hidden $l=2$ có 5 neuron) từ một vector có chiều là 3 (có 3 input). Tương tự, các bạn có thể đoán là ma trận $W^{(3)}$ của lớp Output sẽ có số chiều là $5\times 2$ như sau:

$$W^{(3)} = \left[ {\begin{array}{cc} w_{11}^{(3)} & w_{21}^{(3)}\\ w_{12}^{(3)} & w_{22}^{(3)} \\ w_{13}^{(3)} & w_{23}^{(3)} \\ w_{14}^{(3)} & w_{24}^{(3)} \\ w_{15}^{(3)} & w_{25}^{(3)} \end{array} } \right]$$

vì nó từ một input vector của 5 neuron lớp Hidden $l=2$ output ra một vector có chiều là 2 (2 neuron ở lớp Output). Lưu ý là input vector cho 2 neuron ở lớp Output không phải là $z^{(2)}$ mà là $a^{(2)}$ với:

$$a^{(2)} = \left[ {\begin{array}{c} \sigma(z_{1}^{(2)}) \\ \sigma(z_{2}^{(2)}) \\ \sigma(z_{3}^{(2)}) \\ \sigma(z_{4}^{(2)}) \\ \sigma(z_{5}^{(2)}) \end{array} } \right] = \sigma (z^{(2)}) = \sigma (W^{(2)T}x + b^{(2)})$$

Tóm lại, toàn bộ các tính toán từ đầu vào cho tới đầu ra của một MLP 3 lớp như Hình 1 có thể được tóm tắt như sau:

$$z^{(2)} = W^{(2)T}x + b^{(2)} \\ a^{(2)} = \sigma (z^{(2)}) \\ z^{(3)} = W^{(3)T}a^{(2)} + b^{(3)} \\ \hat{y} = a^{(3)} = f(z^{(3)})$$

Chính vì cách tính toán theo một chiều từ đầu vào cho tới đầu ra như trên mà một MLP như chúng ta đang xét còn được gọi là Feed-forward Neural Network (feedforward: truyền tới). Cần chú ý là đối với neuron ở lớp Output thì tùy vào output của bài toán mà ta sẽ chọn Activation function $f$ cho phù hợp. Ví dụ cụ thể về một số loại bài toán và cách chọn activation function cho lớp Output sẽ được đề cập trong bài viết tiếp theo.

4. Kết bài

Vậy là trong phần 2 này chúng ta đã cùng tìm hiểu về một mạng Neural Network đơn giản nhất trong DL là MLP được xây dựng nên từ các perceptron mà ta đã tìm hiểu ở phần 1. Nhóm đã giới thiệu qua về các kí hiệu được dùng để biểu diễn MLP nói riêng và trong các mạng NN khác nói chung như input vector, output vector, layer, weight matrix, bias vector… Tuy nhiên chúng ta vẫn chưa biết làm thế nào để giúp một MLP học và nó có thể làm được những gì. Đây cũng sẽ là chủ đề của bài viết tiếp theo trong series mà ở đó nhóm sẽ tiếp tục giới thiệu về các khái niệm cơ bản khác như Loss function, Gradient Descent và Backprobagation.

hito.gen